La proportionnalité
x, y, t et k sont des nombres relatifs.
1) Représentation graphique d'une situation de proportionnalité:
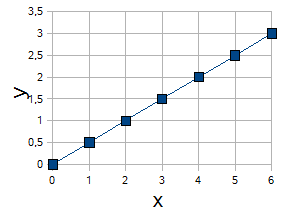
Si deux grandeurs sont proportionnelles elles sont représentées graphiquement dans un repère par des points alignés avec l'origine du repère.
Exemple:
|
x |
2 |
3 |
4 |
6 |
|---|---|---|---|---|
|
y |
1 |
1,5 |
2 |
3 |
y = 0,5x
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|---|
|
y |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
Si deux grandeurs sont représentées graphiquement dans un repère par des points alignés avec l'origine du repère, alors elles sont proportionnelles.
Un tableau représente une situation de proportionnalité si on passe d'une ligne à l'autre en multipliant toujours par le même nombre appelé coefficient de proportionnalité.
Dans l'exemple, le coefficient de proportionnalité est 0,5. y = 0,5x
2) Pourcentages:
Augmenter une quantité
de t % revient à multiplier cette quantité par 
.
Une boite de 400 g est vendue avec 25% de produit en plus, sa nouvelle masse, en grammes est
m=500g
Diminuer une quantité de
t % revient à multiplier cette quantité par 
.
En France une baisse de 4% a été enregistrée sur un effectif annuel de 750 000 naissances.
Le
nouvel effectif est 
3) Exemples de grandeurs composées:
a) Grandeurs quotients:
le prix au litre d'un liquide
est le quotient du prix P (en €) du liquide par son volume V (en L) 
en
euro par litre (€.L-1).
La densité de population
d'un pays est le quotient du nombre N de ses habitants par sa superficie S (en
km²) 
en habitants par km² (habitants.km-²).
b) Grandeurs produits:
L'aire d'un rectangle s'exprime en fonction de sa longueur L (en m) et de sa largeur (l) (en m) par le produit A=L ´ l en mètres carrés (m²).
Le volume d'un cube de côté c s'exprime en fonction de c (en m) par le produit V=c´c´c=c3 en mètres cubes (m3).
c) Grandeurs dérivées:
La puissance p reçue du Soleil par unité de surface sur la Terre est le quotient de la puissance P émise par le Soleil, par l'aire A de la Terre dont le rayon est R (en m)
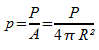p est une grandeur dérivée
dont l'unité est watt par mètre carré (Wm-²).
4) Réduction et agrandissement:
Quand on agrandit (k>1) ou on réduit (0<k<1) une figure, si les dimensions sont multipliées par k alors l'aire est multipliée par k².
Quand on agrandit ou on réduit un solide, si les dimensions sont multipliées par k alors le volume est multiplié par k3.