Le théorème de Thalès
1) Rappels:
Si deux droites sont perpendiculaires à une même troisième alors elles sont parallèles entre elles.
Si deux droites sont parallèles avec un point commun alors elles sont confondues
2) Les situations de Thalès:
d et d' sont deux droites sécantes en A et les droites (BC) et (MN) sont parallèles.
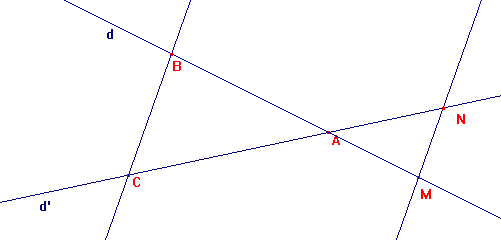
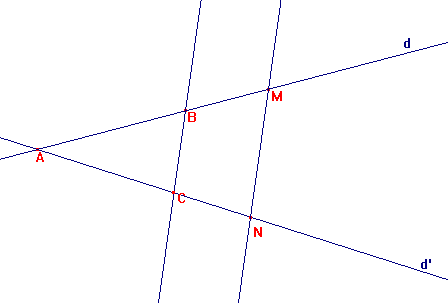
3) Le théorème de Thalès:
Soit (d) et (d') deux droites sécantes en A.
Soit B et M deux points de (d) distincts de A.
Soit C et N deux points de (d') distincts de A
Si les droites (BC) et (MN) sont parallèles, alors
Remarques : Si les rapports 
sont
différents alors les droites (BC) et (MN) ne sont pas parallèles.
Pour écrire les rapports :
4) La réciproque du théorème de Thalès:
Soit (d) et (d') deux droites sécantes en A.
Soit B et M deux points de (d) distincts de A.
Soit C et N deux points de (d') distincts de A.
Si
et si les points A, B, M et les points A, C, N sont dans le même ordre, alors les droites (BC) et (MN) sont parallèles.
5) Exemples:
Le Théorème de Thalès:
On utilise dans les calculs la technique des "produits en croix":
ABC est un triangle avec AB=4cm; AC=5cm et BC=6cm.
Sur le segment [AB] on place M tel que BM=3cm. La parallèle à (AC) passant par M coupe (BC) en N.
Calculer BN et MN.
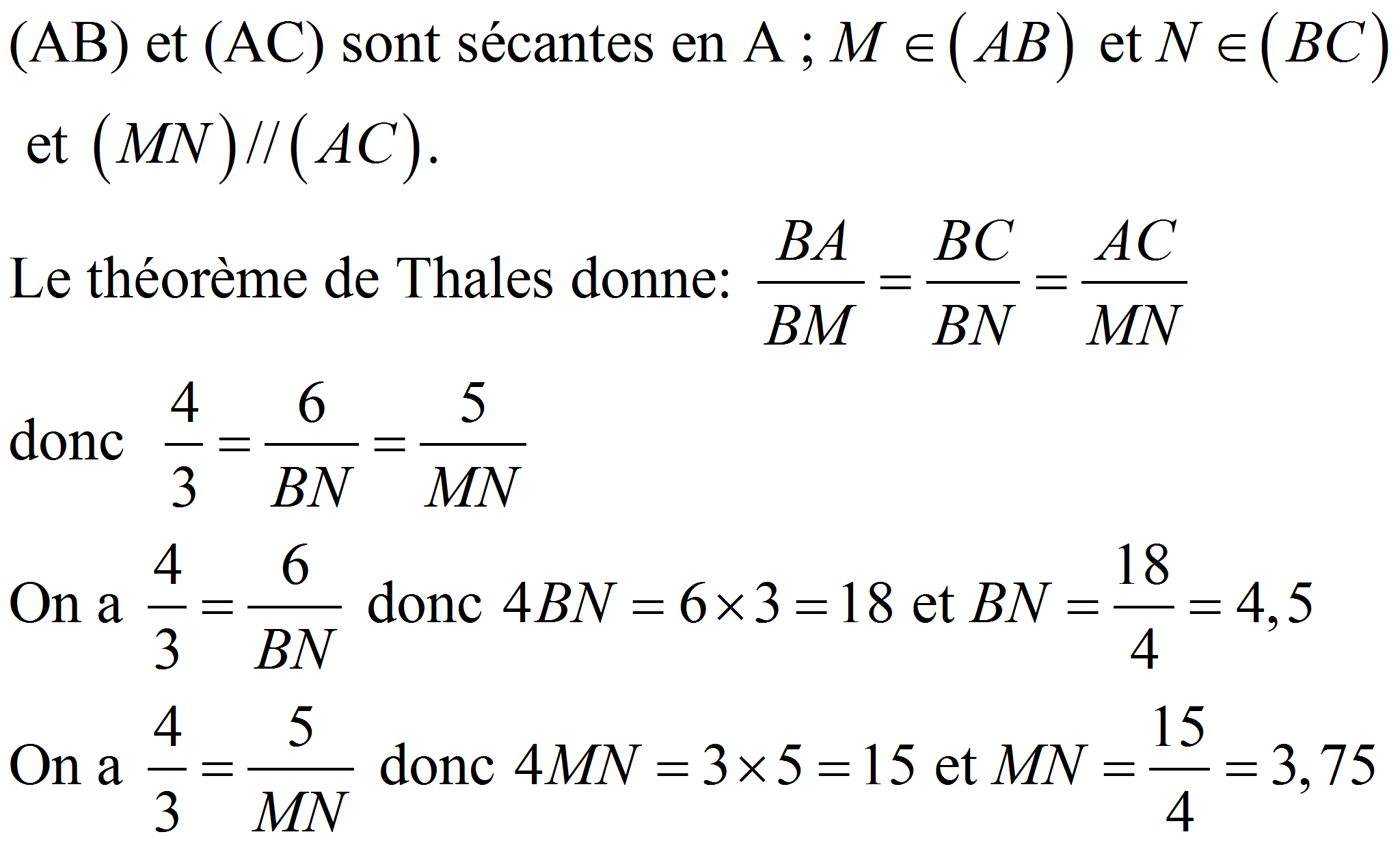
La réciproque du Théorème de Thalès:
Soit (C1) et (C2) deux cercles de même centre O et de rayons r1 et r2.
Une demi-droite D issue de O coupe (C1) en A et (C2) en B.
Une demi-droite D' issue de O coupe (C1) en M et (C2) en N. Démontrer que les droites (AM) et (BN) sont parallèles.
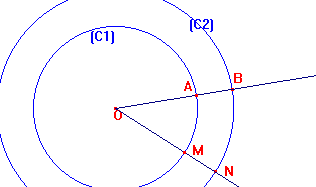
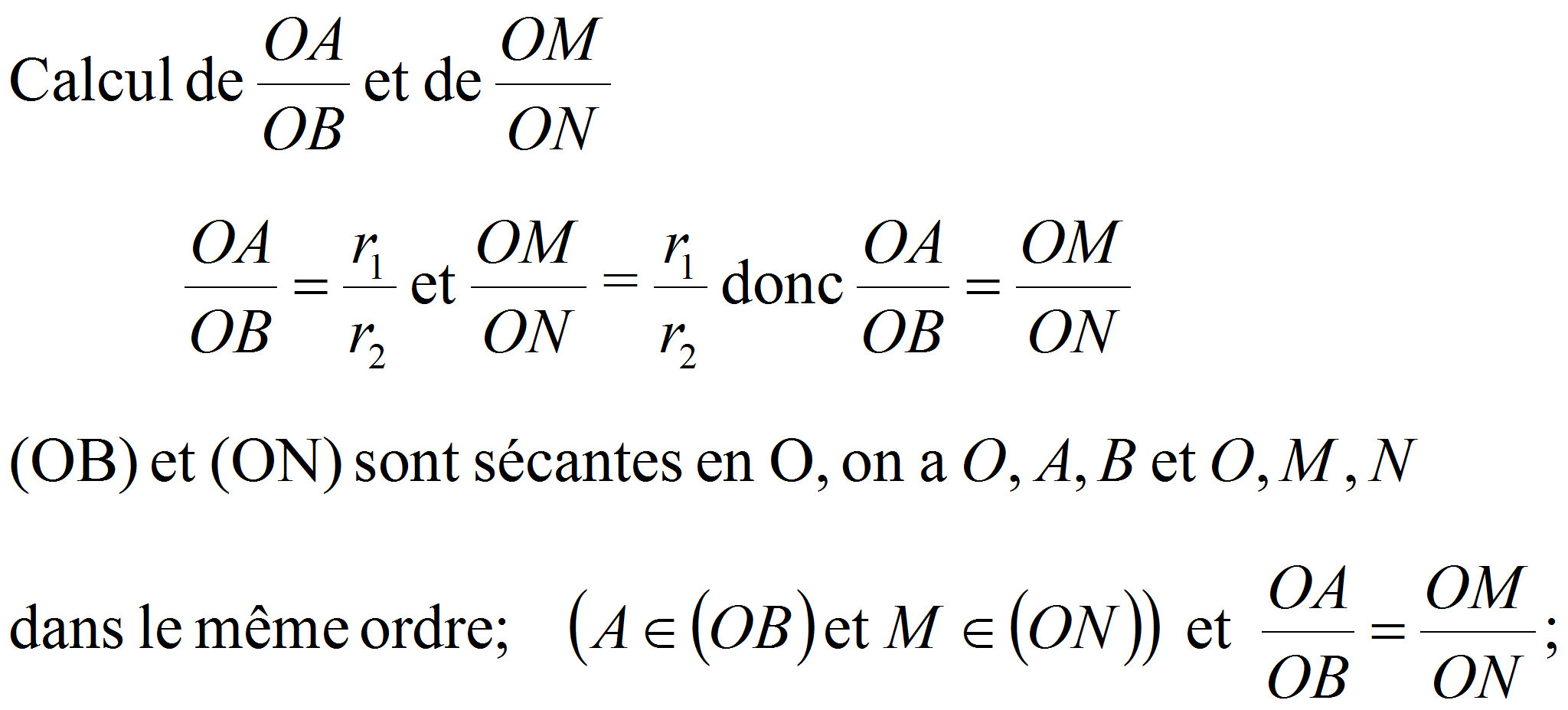
la réciproque du théorème de Thalés donne (AM)//(BN).
