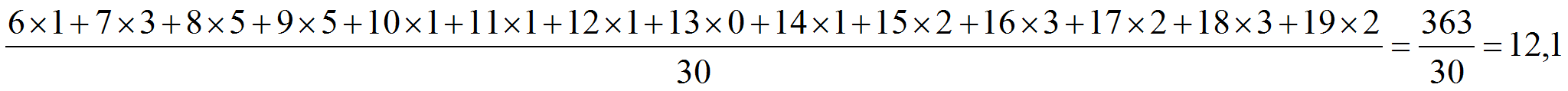
Statistiques
Les notes obtenues à un devoir sont:
10, 6, 17, 14, 8, 7, 16, 8, 17, 8, 11, 8, 18, 18, 9, 16, 8, 7, 12, 19, 7, 9, 15, 9, 9, 15, 9, 16, 18, 19.
1) Tableau:
|
Notes |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Effectifs |
1 |
3 |
5 |
5 |
1 |
1 |
1 |
0 |
1 |
2 |
3 |
2 |
3 |
2 |
|
Effectifs cumulés |
1 |
4 |
9 |
14 |
15 |
16 |
17 |
17 |
18 |
20 |
23 |
25 |
28 |
30 |
|
Effectifs décumulés |
30 |
29 |
26 |
21 |
16 |
15 |
14 |
13 |
13 |
12 |
10 |
7 |
5 |
2 |
|
Fréquence % |
3,3 |
10 |
16,6 |
16,6 |
3,3 |
3,3 |
3,3 |
0 |
3,3 |
6,6 |
10 |
6,6 |
10 |
6,6 |
Calcul de la fréquence : (effectif ´total):100 (le total des fréquences doit être très proche de 100)
Etendue (ou amplitude) d'une série :
La différence entre la plus grande valeur et la plus petite valeur de la variable (ici la note) donne l'étendue (ou l'amplitude) de la série.
Ici l'étendue
(ou l'amplitude) est (19-6=13) 13.
Effectifs cumulés :
Calcul des effectifs cumulés: Calcul des effectifs décumulés :
|
Effectifs |
1 |
3 |
5 |
5 |
|
|
Effectifs |
|
3 |
2 |
3 |
2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Effectifs cumulés |
1 |
4 |
9 |
14 |
|
|
Effectifs décumulés |
|
10 |
7 |
5 |
2 |
Si on regarde les effectifs cumulés, on peut répondre aux questions du genre : combien y a-t-il de notes égales ou inférieures à 10 ? réponse 15.
Si on regarde les effectifs décumulés, on peut répondre aux questions du genre : combien y a t-il de notes égales ou supérieures à 10 ? réponse 16.
2) Calcul de la moyenne: 12,1
Méthode 1: on additionne toutes les notes et on divise par le nombre de notes.
C'est la méthode à utiliser quand on a la liste des valeurs.
Méthode 2: on utilise le tableau et on additionne (note)(effectifs) puis on divise par le nombre de notes. Dans ce cas on dit que l'on a fait un calcul pondéré.
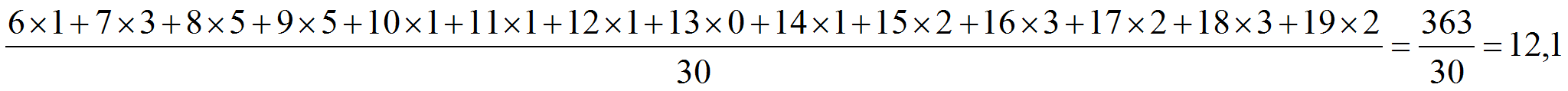
3) Médiane : 10,5

La médiane est la note permettant de séparer l'effectif total en deux effectifs égaux (ici 10,5 est la note qui partage l'effectif total de 30 en deux parties égales).
On peut dire que 15 élèves ont 10,5 ou moins et que 15 élèves ont 10,5 ou plus.
En général la médiane et la moyenne sont différentes.
Pour trouver la médiane, pratiquement :
Ranger les valeurs dans l'ordre croissant :
6, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 11, 12, 14, 15, 15, 16, 16, 16, 17, 17, 18, 18, 18, 19, 19.
la médiane est la valeur qui partage la série en deux parties égales :
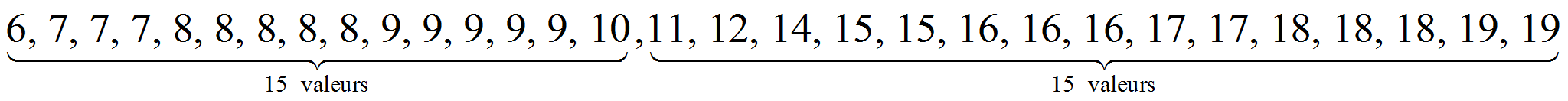
La médiane est entre 10 et 11, on prend donc 10,5.
Remarque :
Si la série a un nombre pair de valeurs, la médiane n'est pas une valeur de la série, on prend une valeur intermédiaire, comme dans notre exemple.
Si la série a un nombre impair de valeurs, la médiane est une valeur de la série.
Exemple : on a la série 3, 4, 5, 5, 6, 7, 7, 8, 8, 9, 10. Elle comporte 11 valeurs.
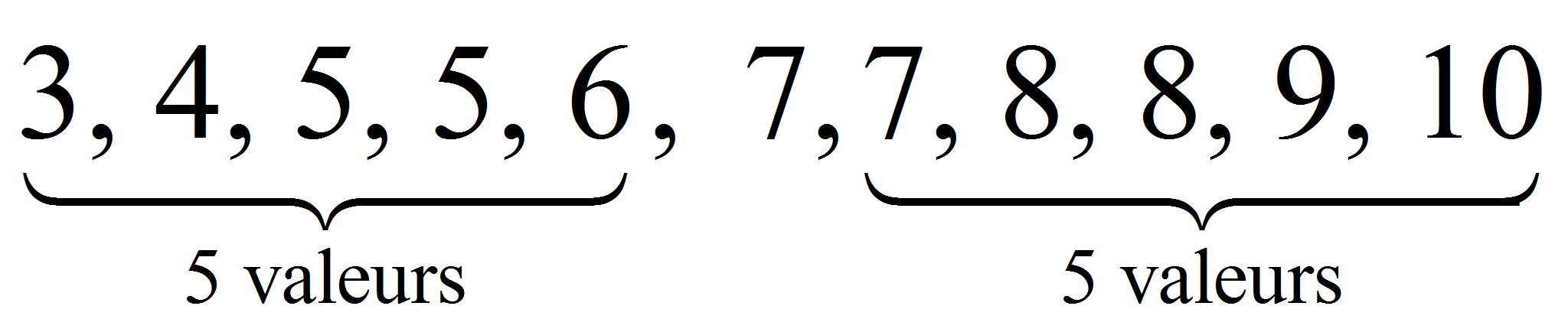
La médiane est 7.
4) Quartiles :
Pour une série, rangée dans l'ordre croissant, on appelle premier quartile la valeur pour laquelle 25% des données lui sont inférieures.
Pour une série, rangée dans l'ordre croissant, on appelle troisième quartile la valeur pour laquelle 75% des données lui sont inférieures.
Pour trouver les quartiles, pratiquement :
on range les valeurs de la série dans l'ordre croissant :
6, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 11, 12, 14, 15, 15, 16, 16, 16, 17, 17, 18, 18, 18, 19, 19.
on partage l'effectif en 4 parties égales : comme![]() , on partage ici par tranches de 7 valeurs :
, on partage ici par tranches de 7 valeurs :
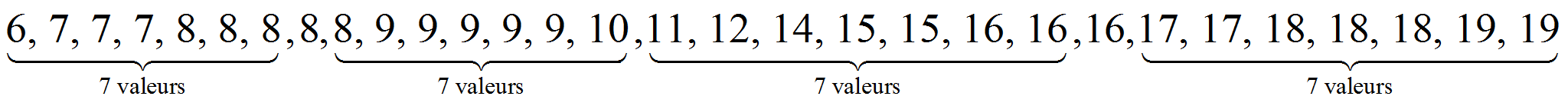
Le premier quartile est 8. Un quart (25%) des valeurs sont inférieures à 8.
(Ici 7 valeurs sont inférieures à 8).
Le troisième quartile est 16. Trois quarts (75%) des valeurs sont inférieures à 16.
(Ici 22 valeurs sont inférieures
à 16).
