Géométrie dans l'espace et sphère.

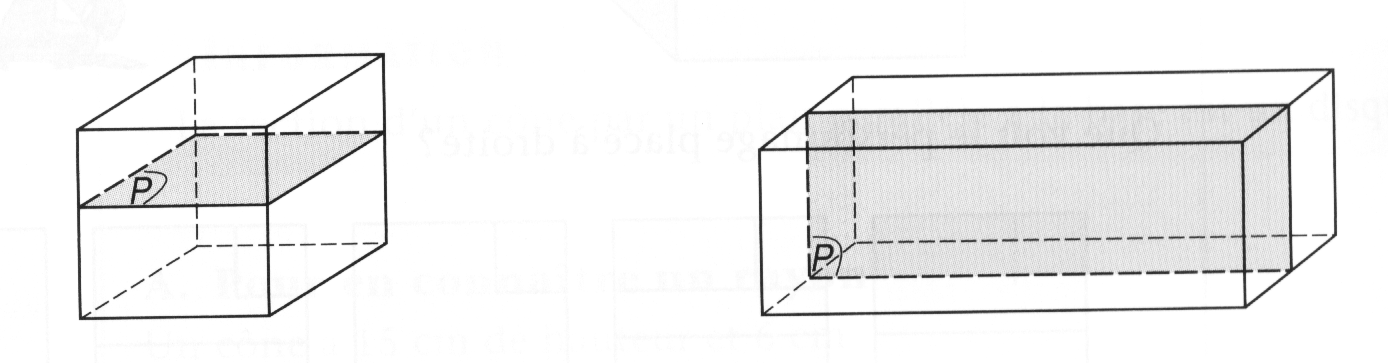
1) Cube, parallélépipède :

La section d'un cube ou d'un parallélépipède par un plan parallèle à une face est un carré ou un rectangle ayant les mêmes dimensions que cette face.

La section d'un cube ou d'un parallélépipède par un plan parallèle à une arête est un rectangle.

2) Cylindre:

La section d'un cylindre par un plan perpendiculaire à l'axe du cylindre est un disque de même rayon que la base. (fig 1)

fig 1

La section d'un cylindre par un plan parallèle à l'axe du cylindre est un rectangle. (fig 2)

Dans le cas particulier où le plan contient l'axe du cylindre, la section est un rectangle de dimensions h et 2R. (fig 3)

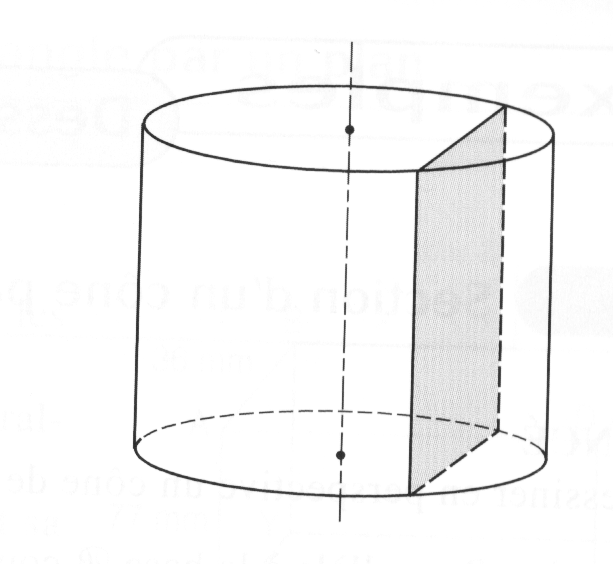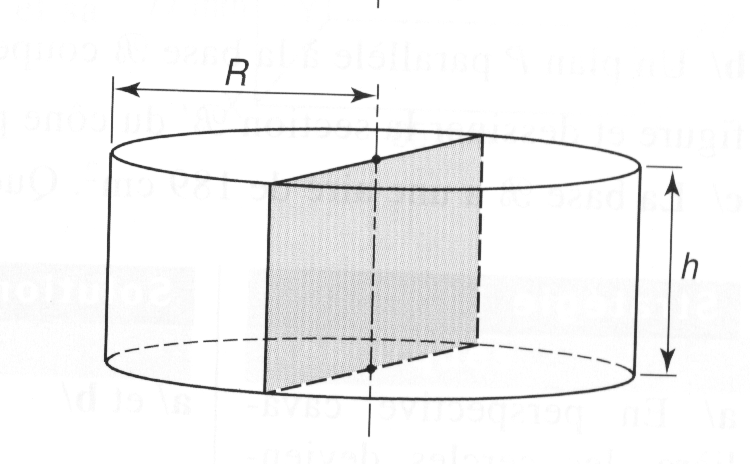fig 2 fig 3

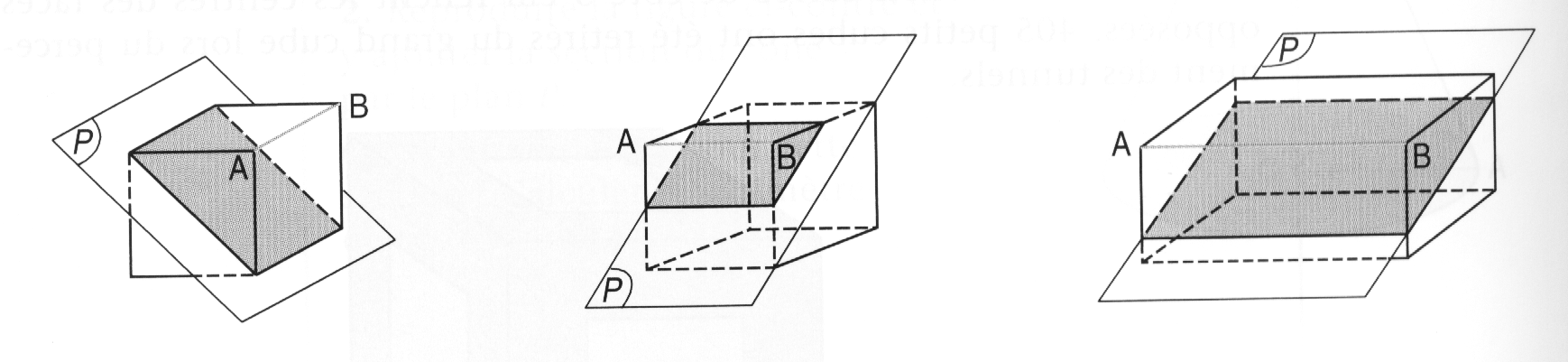
3) Cône, pyramide :

La section d'un cône par un plan parallèle à la base est un disque qui est une réduction du disque de base. Le rapport de réduction est .

La section d'une pyramide par un plan parallèle à la base est un polygone qui est une réduction du polygone de la base. Le rapport de réduction est .

4) Sphère :

La sphère de centre O et de rayon R est l'ensemble des points de l'espace dont la distance à O est égale à R.

La boule de centre O et de rayon R est l'ensemble des points de l'espace dont la distance à O est inférieure ou égale à R.

Deux points d'une sphère sont diamétralement opposés si le centre de la sphère est le milieu du segment joignant ces deux points.

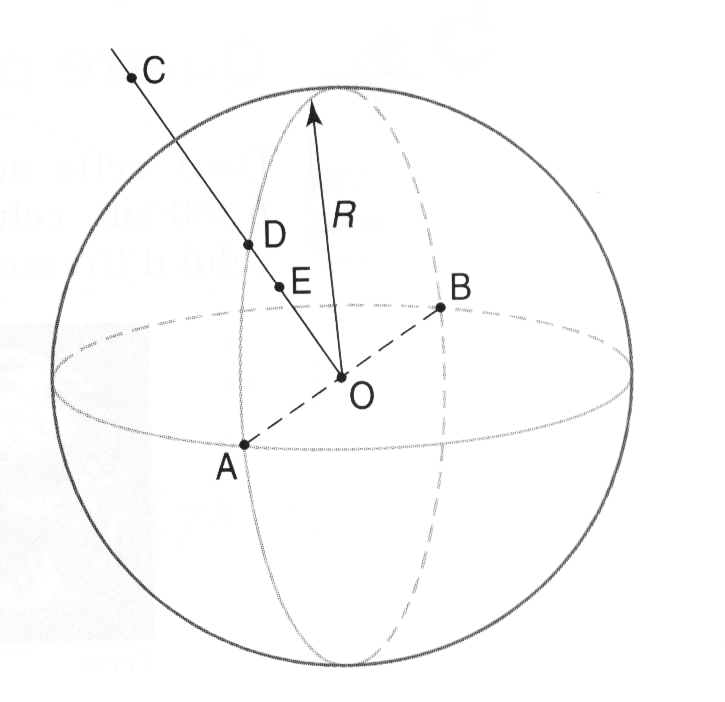
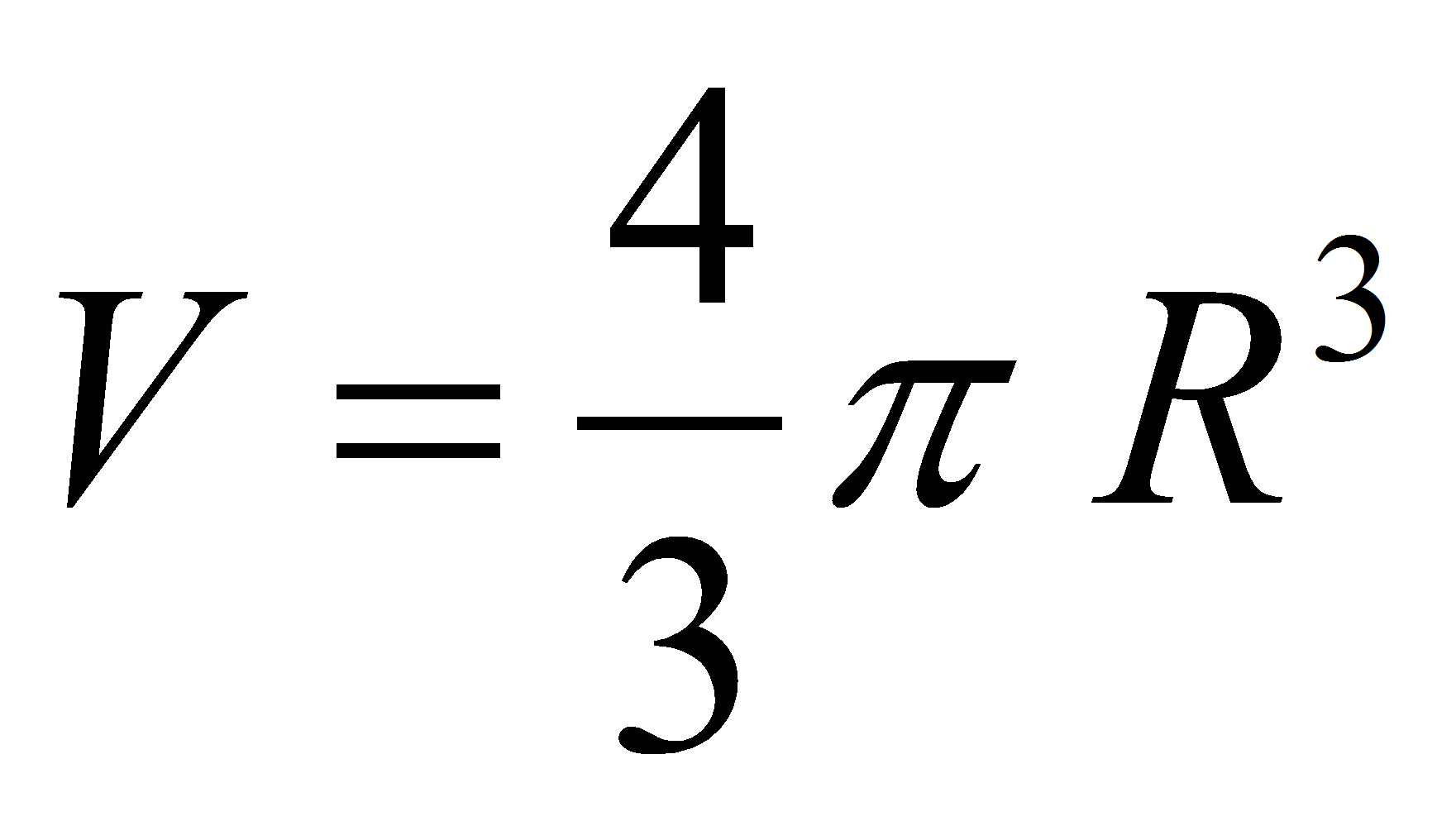
La section d'une sphère par un plan est un cercle.

Quand ce plan passe par le centre de la sphère on dit que la section est un grand cercle.

Si on connaît la distance OO' et le rayon R de la sphère, on peut trouver le rayon de la section de la sphère en utilisant Pythagore :

OO'² + r² = R² et r² = R² – OO'² .

Donc

5) Formulaire:

L'aire d'une sphère de rayon R est A = 4pR².

Le volume d'une boule de rayon R est .

Le volume d'une pyramide de hauteur h est .

Le volume d'un cône de rayon de base R et de hauteur h est.

Le volume d'un cylindre de rayon de base R et de hauteur h est V = pR²h.