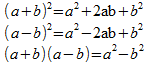Compétences troisième
1. Organisation et gestion de données, fonctions
1.1 Notion de fonction:
Déterminer l'image d'un nombre par une fonction déterminée par une courbe, un tableau de données ou une formule.
1.2 Fonction linéaire, fonction affine :
Proportionnalité; fonction linéaire:
Déterminer par le calcul l'image d'un nombre donné et l'antécédent d'un nombre donné.
Déterminer l'expression algébrique d'une fonction linéaire à partir de la donnée d'un nombre non nul et de son image.
Représenter graphiquement une fonction linéaire.
Lire sur la représentation graphique d'une fonction linéaire l'image d'un nombre donné et l'antécédent d'un nombre donnée.
Fonction affine :
Déterminer par le calcul l'image d'un nombre donné et l'antécédent d'un nombre donné.
Déterminer une fonction affine à partir de la donnée de deux nombres et de leurs images.
Représenter graphiquement une fonction affine.
Lire sur la représentation graphique d'une fonction affine l'image d'un nombre donné et l'antécédent d'un nombre donnée.
1.3 Statistique
Caractéristiques de position :
Une série statistique étant donnée (sous forme de liste ou de tableau ou par une représentation graphique ) :
Déterminer une valeur médiane de cette série et en donner la signification ;
déterminer des valeurs pour les premier et troisièmes quartile et en donner la signification ;
déterminer son étendue.
Exprimer et exploiter les résultats de mesures d'une grandeur.
1.4 Notion de probabilité :
Comprendre et utiliser des notions élémentaires de probabilité.
Calculer des probabilités dans des contextes familiers.
2. Nombres et calculs
2.1 Nombres entiers et rationnels :
Opérations sur les nombres relatifs en écriture fractionnaire.
Diviseurs communs à deux entiers :
Déterminer si deux entiers donnés sont premiers entre eux.
Fractions irréductibles :
Simplifier une fraction donnée pour la rendre irréductible.
2.2 Calculs élémentaires sur les radicaux :
Racine carrée d'un nombre positif :
Savoir que si a
désigne un nombre positif, 
est
le nombre positif dont le carré est a.
Sur des exemples numériques où a est un nombre positif, utiliser les égalités:
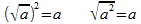
Déterminer, sur des exemples numériques les nombres x tels que x²=a, où a désigne un nombre positif.
Produit et quotient de deux radicaux :
Sur des exemples numériques, où a et b sont deux nombres positifs, utiliser les égalités:
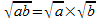
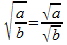(b non nul).
2.3 Ecritures littérales :
Puissances :
Utiliser sur des exemples les égalités :
;
;
;
;
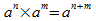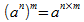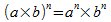où a
et b
sont des nombres non nuls et m et
n des entiers relatifs.
Factorisation :
Connaître dans le cas général la factorisation des expressions algébriques dans lesquelles le facteur est apparent.
Identités remarquables:
Connaître les identités :
Les utiliser dans les deux sens sur des exemples numériques ou littéraux simples.
2.4 Equations et inéquations du premier degré:
Problèmes du premier degré: inéquation du premier degré à une inconnue, système de deux équations à deux inconnues :
Mettre en équation un problème.
Résoudre une inéquations du premier degré à une inconnue à coefficients numériques; représenter ses solutions sur une droite graduée.
Résoudre algébriquement un système de deux équations à deux inconnues admettant une solution et une seule; en donner une interprétation graphique.
Problèmes se ramenant au premier degré : équation produit :
Résoudre un équation mise sous la forme A(x).B(x)=0, où A(x) et B(x) sont deux expressions du premier degré de la même variable x.
3 Géométrie.
3.1 Figures planes :
Triangle rectangle, relations trigonométriques :
Connaître et utiliser dans le triangle rectangle les relations entre le cosinus, le sinus ou la tangente d'un angle aigu et les longueurs de deux des côtés d'un triangle rectangle.
Déterminer à l'aide d'une calculatrice, des valeurs approchées :
du sinus, du cosinus et de la tangent d'un angle aigu donné;
de l'angle aigu dont on donne le sinus, le cosinus ou la tangente.
Configuration de Thalès :
Connaître et utiliser dans une situation donnée les deux théorèmes suivants :
soit B et M deux points de d, distincts de A,
soit C et N deux points de d', distincts de A;
si les droites (BC) et (MN) sont parallèles ;
alors
soient B et M deux points de d, distincts de A,
soient C et N deux points de d', distincts de A;
si
et si les points A,B,M et les points A,C,N sont dans le même ordre;
alors les droites (BC) et (MN) sont parallèles.
Agrandissement et réduction : (reprise du programme de quatrième)
Agrandir ou réduire une figure en utilisant la conservation des angles et la proportionnalité entre les longueurs de la figure initiale et celles de la figure à obtenir.
Angle inscrit, angle au centre :
Connaître et utiliser la relation entre un angle inscrit et l'angle au centre qui intercepte le même arc.
Polygones réguliers :
Construire un triangle équilatéral, un carré, un hexagone régulier connaissant son centre et un sommet.
3.2 Configurations dans l'espace :
Problèmes de sections planes de solides :
Connaître et utiliser la nature des sections du cube, du parallélépipède rectangle par un plan parallèle à une face, à une arête.
Connaître et utiliser la nature des sections du cylindre de révolution par un plan parallèle ou perpendiculaire à son axe.
Connaître et utiliser les sections d'un cône de révolution et d'une pyramide par un plan parallèle à la base.
Sphère :
Connaître la nature de la section d'une sphère par un plan.
Calculer le rayon du cercle d'intersection connaissant le rayon de la sphère et la distance du plan au centre de la sphère.
Représenter une sphère et certains de ses grands cercles.
4. Grandeurs et mesures
4.1 Aires et volumes :
Calculs d'aires et volumes :
Calculer l'aire d'une sphère de rayon donné.
Connaître et utiliser le fait que, dans un agrandissement ou une réduction de rapport k,
l'aire d'une surface est multipliée par k²,
le volume d'un solide est multiplié par k3.
4.2 Grandeurs composées, changement d'unités :
Effectuer des changements d'unités sur des grandeurs produits ou des grandeurs quotients.
Calculer des vitesses moyennes.
