Fonctions linéaires et affines
a, b, x et y sont des nombres relatifs.
1) Rappels sur la proportionnalité , fonctions linéaires :
Voici un tableau de proportionnalité :
|
x |
2 |
3 |
5 |
1,5 |
-2 |
-4 |
0 |
1 |
|---|---|---|---|---|---|---|---|---|
|
y |
7 |
10,5 |
17,5 |
5,25 |
-7 |
-14 |
0 |
3,5 |
Les nombres de la seconde ligne s'obtiennent en multipliant ceux de la première par un même nombre appelé coefficient : ici 3,5.
Si on désigne par x un nombre de la première ligne et par y un nombre de la seconde ligne correspondant on a y=3,5´x
On dit que l'on passe de x à y par la fonction linéaire de coefficient 3,5.
Cette
fonction se note ![]()
Si on appelle f cette fonction linéaire, au nombre 3 on associe la valeur 10,5 ; on dit que 3 a pour image 10,5 et on écrit f(3)=10,5 .
De même f(-2)= -7 ; l'image de -2 est -7.
La représentation graphique d'une fonction linéaire est une droite passant par l'origine du repère.
On dit que la droite D a pour équation y=3,5x ; on dit que 3,5 est le coefficient directeur de la droite D.

On remarque que le
coefficient directeur est ![]()
exemple: ![]()
2) Fonctions affines:
La fonction f qui
a x associe -2x+3 se note ![]() .
.
On dit que f est une fonction affine.
On a le tableau suivant :
|
x |
1 |
0 |
4 |
-1 |
-2 |
3 |
|---|---|---|---|---|---|---|
|
y |
1 |
3 |
-5 |
5 |
7 |
-3 |
L'image de 4 se note f(4) et on a f(4)= -2 ´ 4 + 3 = -5
La représentation graphique d'une fonction affine est une droite D .
Cette droite D a pour équation y= -2x+3 .
On dit que -2 est le coefficient directeur de la droite D ; et que +3 est son ordonnée à l'origine car f(0)=+3 .
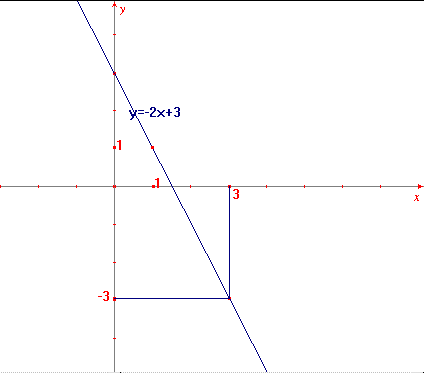
Remarques :
Le coefficient directeur
est ![]()
exemple : ![]()
Une fonction linéaire est une fonction affine particulière , son ordonnée à l'origine est nulle.
Une fonction affine dont le coefficient directeur est nul a une représentation parallèle à l'axe des abscisses.
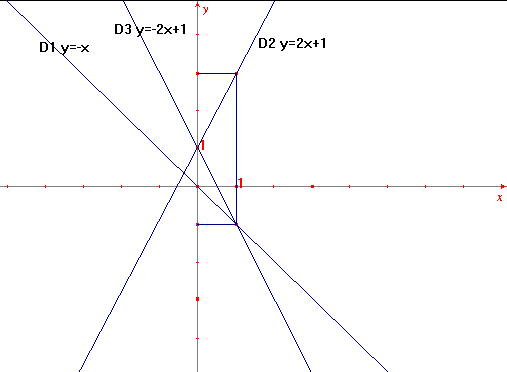
3) Exemples:
| f(x)=-x | g(x)=2x+1 |
h(x)=-2x+1 |
|
Fonction linéaire |
Fonction affine | Fonction affine |
|
f est représentée par D1 d'équation y=-x |
g est représentée par
D2
d'équation y=2x+1 |
h est représentée par D3 d'équation y=-2x+1 |
|
coefficient directeur:-1 |
coefficient directeur:2 | coefficient directeur:-2 |
|
(0;0) et (1,-1) sont des points de D1 |
(0;1) et (1;3) sont des points de D2 | (0;1) et (1,-1) sont des points de D3 |
4) Formules :
Une fonction linéaire est représentée par :
ou f(x)=ax ou y=ax
a nombre fixe
Une fonction affine est représentée par :
ou f(x)=ax+b ou y=ax+b
a et b nombres fixes
Si a>0 la fonction est croissante.
Si a<0 la fonction est décroissante.