La symétrie axiale
1) Symétrique d'un point :
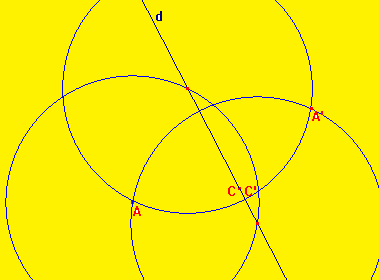
A et A' sont deux points symétriques par rapport à la droite d si A et A' coïncident par pliage sur la droite d.
On dit aussi que A' est le symétrique de A par rapport à la droite d.
Les points de la droite d sont égaux à leurs symétriques.

2) Symétrique d'un segment :
[AB] est un segment, A' est le symétrique de A par rapport à d, B' est le symétrique de B par rapport à d.
Le symétrique du segment [AB] est le segment [A'B']. Ces segments sont de même longueur.
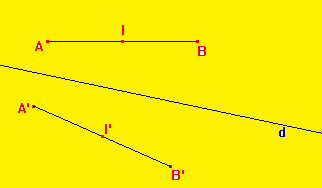
Si I est le milieu du segment [AB], alors
son symétrique I' est le milieu du segment [A'B'].
3) Construction du symétrique d'un point :
A' est le symétrique de A par rapport à d,
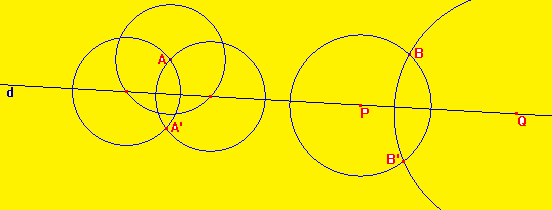
4) Symétrique d'une figure :
Si des points A, B et C sont alignés, alors leurs symétriques A', B' et C' sont alignés.
En pliant autour de la droite d deux figures symétriques se superposent.
A et A' sont symétriques par rapport à la droite d.
A' est la figure symétrique de A par rapport à d.
Deux figures symétriques par rapport à une droite ont même périmètre et même aire.
5) Médiatrice d'un segment :
Définition 1 : La médiatrice d'un segment est la droite perpendiculaire au milieu du segment.
Définition 2 : La médiatrice d'un segment est constituée de tous les points qui sont à égale distance des extrémités du segment.
La médiatrice d'un segment est l'axe de symétrie de ce segment.
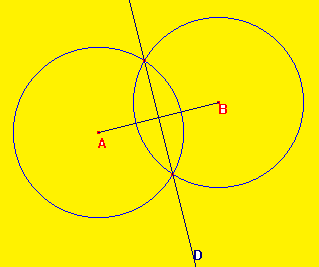
La droite D est la médiatrice du
segment [AB].
6) Bissectrice d'un angle :
La bissectrice d'un angle est la demi-droite qui partage cet angle en deux parties égales.
La bissectrice d'un angle est l'axe de symétrie des côtés de l'angle.
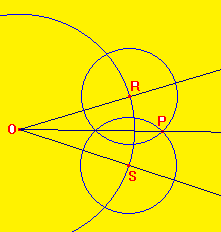
La demi-droite [OP) est la bissectrice de RÔS.
7) Propriétés de conservation :
Deux segments symétriques par rapport à une droite ont même longueur.
Deux angles symétriques par rapport à une droite ont même mesure.
Les symétriques par rapport à une droite de deux droites perpendiculaires sont perpendiculaires.
Les symétriques par rapport à une droite de deux droites parallèles sont parallèles.