Cercles, triangles, quadrilatères

1) Des triangles particuliers :

Triangle rectangle:

(AB)^(AC); le triangle est rectangle en A

Un triangle rectangle a deux côtés perpendiculaires.

Triangle isocèle:

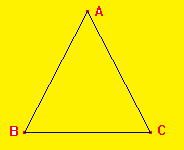
AB=AC; le triangle est isocèle en A

Un triangle isocèle a deux côtés de même longueur.

Triangle équilatéral:

AB=AC=BC

Un triangle équilatéral a ses trois côtés de même longueur.

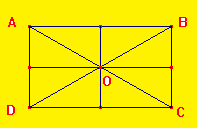
2) Le rectangle :

Un quadrilatère est une figure fermée à quatre côtés.

Un quadrilatère ayant ses angles droits est un rectangle.

Dans un rectangle:

- les côtés consécutifs sont perpendiculaires;

- les côtés opposés sont de même longueur;

- les côtés opposés sont parallèles;

- les diagonales sont de même longueur;

- les diagonales se coupent en leur milieu, appelé centre du rectangle;

- les médianes sont perpendiculaires;

- les médianes se coupent en leur milieu, centre du rectangle;

3) Le losange :

Un losange est un quadrilatère qui a ses côtés de même longueur.

Un losange possède deux axes de symétrie perpendiculaires: ses diagonales.

Un losange a ses angles opposés de même mesure.

Un losange a ses côtés opposés parallèles.

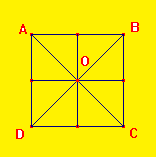
4) Le carré :

Un carré est un rectangle particulier: ses côtés sont tous de même longueur.

Un carré est un losange particulier: ses angles sont droits.

Un carré est donc à la fois un rectangle et un losange, il possède les propriétés des deux figures.

5) Le cerf-volant :

Un cerf-volant est un quadrilatère formé de deux triangles isocèles de même base.

Un cerf-volant a une diagonale qui est médiatrice de l'autre diagonale,

6) Le cercle:

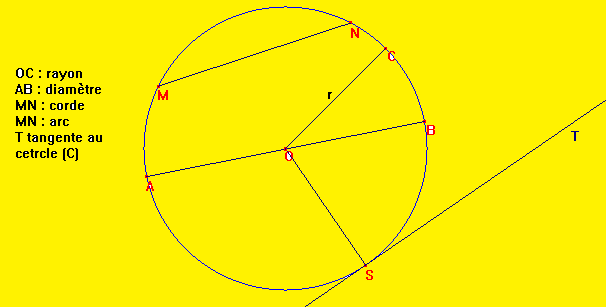
Définitions: (C) : cercle de centre O et de rayon r.

Si A est un point du cercle de centre O et de rayon r, alors OA = r