Les droites remarquables dans le triangle

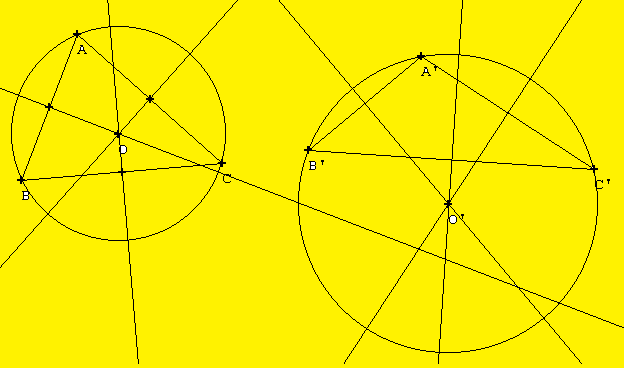
1) Médiatrices, cercle circonscrit:

Rappels: La médiatrice du segment [AB] est la droite perpendiculaire au milieu du segment [AB].

Tout point de la médiatrice d'un segment est équidistant des extrémités de ce segment. Propriété: Les médiatrices des trois côtés d'un triangle se coupent en un même point. Ce point, équidistant des trois sommets du triangle, est le centre du cercle circonscrit au triangle.

L

Le cercle circonscrit au triangle

2) Bissectrices, cercle inscrit :

Rappels: La bissectrice de l'angle est la demi-droite issue de A qui partage l'angle en deux angles de même mesure.

La bissectrice de l'angle est axe symétrie pour cet angle.

Propriété: Les bissectrices des trois angles d'un triangle se coupent en un même point. Ce point , équidistant des trois côtés du triangle, est le centre d'un cercle tangent aux trois côtés: le cercle inscrit dans le triangle.

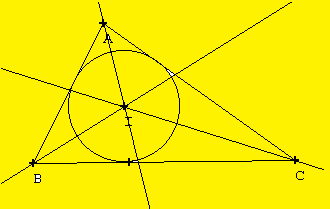
Le cercle inscrit dans le triangle

3) Hauteurs, orthocentre :

Rappel: on appelle hauteur d'un triangle une droite issue d'un sommet et perpendiculaire au côté opposé à ce sommet.

Propriété: Les trois hauteurs d'un triangle se coupent en un même point. Ce point s'appelle l'orthocentre du triangle.

L'orthocentre du triangle

4) Médianes, centre de gravité :

Rappel: on appelle médiane d'un triangle une droite issue d'un sommet passant par le milieu du côté opposé à ce sommet.

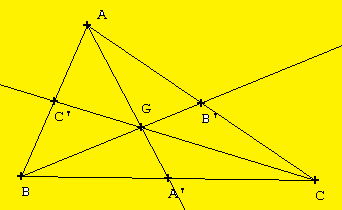
Propriété: Les trois médianes d'un triangle se coupent en un même point. Ce point s'appelle centre de gravité du triangle. Ce point est situé aux deux tiers des segments qui joignent les sommets aux milieux des côtés opposés à ces sommets.

Le centre de gravité du triangle