Comparaisons de nombres

a,b,c, et x désignent des nombres relatifs.

1) Comparaison de nombres relatifs :

a) Signe de la différence:

Comparer deux nombres revient à étudier le signe de leur différence.

Dire que a<b signifie que (a-b)<0

Dire que a=b signifie que (a-b)=0

Dire que a>b signifie que (a-b)>0

b) Pour comparer des nombres en écriture fractionnaire on peut les réduire au même dénominateur.

c) Pour vérifier que deux fractions sont égales, on peut utiliser l'équivalence (b et d étant non nuls).

2) Addition et ordre :

Propriété: Dire que a+b<a+c revient à dire que b<c.

Dire que a+b>a+c revient à dire que b>c.

3) Multiplication et ordre :

Propriété: Si a est nombre positif, non nul, alors

dire que b<c revient à dire que ab<ac ,

dire que b>c revient à dire que ab>ac.

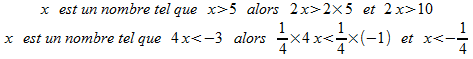
Attention!: 2<3 mais 2´(-5)=-10 et 3´(-5)=-15 alors 2´(-5)>3´(-5)

4) Encadrements et valeurs approchées :

Encadrement: Pour indiquer que x est compris entre a et b inclus, on écrit

On dit que l'on a un encadrement de x d'amplitude (b-a).

Troncature, arrondi:

La troncature de x au millièmes est 3,142.

Cela veut dire que 3,142 £ x £ 3,143 ; (l'amplitude de l'intervalle est 0,001).

L'arrondi au millièmes est 3,143.

Cela veut dire que 3,1425 £ x £ 3,1435 ; (l'amplitude de l'intervalle est 0,001).