Des expressions numériques

a,b,c,d, k et x désignent des nombres relatifs.

1) Suppression de parenthèses :

Règle : Dans une suite d'additions et de soustractions, on peut supprimer des parenthèses précédées du signe + (ainsi que ce signe +), sans changer l'expression entre parenthèses.

ex: a + (b + c) = a + b + c

a + (- b + c) = a - b + c

(a + b) - c = a + b - c

Règle : Dans une suite d'additions et de soustractions, on peut supprimer des parenthèses précédées du signe - (ainsi que ce signe -), en changeant les signes écrits dans l'expression entre parenthèses.

ex: a - (b + c) = a - b - c

a - (- b + c) = a + b - c

2) Distributivité :

k(a + b) = ka + kb

k(a - b) = ka - kb

ex: 3(2x + 5) = 3´2x + 3´5

= 6x + 15

5(4 - 3x) = 5´4 - 5´3x

= 20 -15x

3) Réduction d'une expression littérale :

Réduire une expression littérale, c'est l'écrire avec le moins de termes possibles.

ex: réduction de A=3x²+x-(x²+4x-1)

A=3x²+x-x²-4x+1 (règle de suppression des parenthèses avec -)

A=3x²-x²+x-4x+1 (on met ensemble les x²; les x )

A=(3-1)x²+(1-4)x+1 (on utilise la distributivité)

A=2x²+(-3)x+1

A=2x²-3x+1

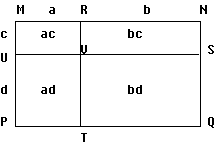
4) Développement de (a+b)(c+d) :

Remarque: Aire (MNPQ) = Aire (MRVU)+Aire (UVTP)+Aire (RNSV)+Aire (VSQT)

(a+b)(c+d) = ac + ad + bc + bd

(a+b)(c+d)=ac+ad+bc+bd

Cette égalité est vraie pour toutes les valeurs de a, b, c et d; on dit que c'est une identité.

ex: développement et réduction de B = (x + 5)(2x + 1)

B = x´2x + x´1 + 5´2x + 5´1 (développement)

B = 2x² + x + 10x + 5 (calcul)

B = 2x² + (1 + 10)x + 5 (réduction)

B = 2x² + 11x + 5