Angles
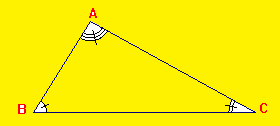
1) Somme des angles d'un triangle :
La somme des mesures des angles d'un triangle est 180°.

![]()
Dans un triangle équilatéral, les angles mesurent 60°.
Dans un triangle équilatéral les trois angles ont même mesure,
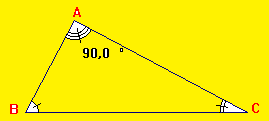
Dans un triangle rectangle, la somme des deux angles aigus est égale à 90°
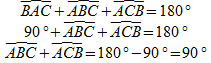
2) Définitions :
Deux angles sont adjacents s'ils ont le même sommet, un côté commun et s'ils sont de part et d'autre de ce côté commun.

![]()
Deux angles sont complémentaires quand la somme de leurs mesures est 90°.
Dans un triangle rectangle les deux angles non droit sont complémentaires.
Deux angles sont supplémentaires quand la somme de leurs mesures est 180°.
3) Triangle isocèle, triangle équilatéral :
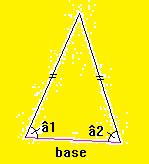
Dans un triangle isocèle, les angles à la base ont même mesure.
Si le triangle est isocèle : â1=â2.
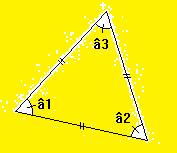
Si un triangle a deux angles égaux, alors il est isocèle.
Si dans le triangle â1=â2 ; alors il est isocèle.
Dans un triangle équilatéral, les trois angles ont même mesure.
Si le triangle est équilatéral : â1=â2=â3
Si un triangle a trois angles égaux, alors il est équilatéral.
Si dans le triangle â1=â2=â3 ; alors il est équilatéral.
4) Angles formés par deux parallèles et une sécante :
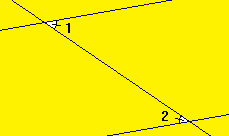
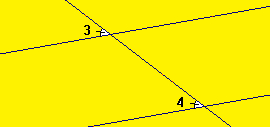
1 et 2 sont des angles alternes-internes. 3 et 4 sont des angles correspondants.
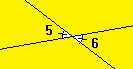
5 et 6 sont des angles opposés par le sommet.
Deux angles opposés par le sommet ont même mesure.
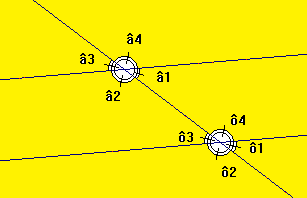
Si deux droites parallèles sont coupées par une sécante, alors :
les angles alternes-internes sont égaux ;
â1=ô3 et â2=ô4
les angles correspondants sont égaux.
â3=ô3 et â4=ô4
â2=ô2 et â1=ô1
Dans tous les cas les angles opposés par le sommet sont égaux:
â1=â3 et â2=â4 ; ô1=ô3 et ô2=ô4
5) Conditions de parallélisme :
Si deux droites sont coupées par une sécante en formant des angles alternes-internes égaux, alors ces droites sont parallèles.
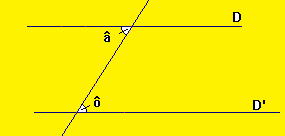
Si â=ô alors D//D'
Si deux droites sont coupées par une sécante en formant des angles correspondants égaux, alors ces droites sont parallèles.
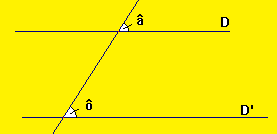
Si â=ô alors D//D'