Parallèles et perpendiculaires. Constructions

(AB): droite passant par les points A et B

[AB]: segment d'extrémités A et B.

[AB) : demi-droite d'origine A passant par B

AB: longueur du segment [AB].

"appartient à" ou "est élément de "

1) Droites :

Par deux points distincts A et B, il ne passe qu'une seule droite : la droite (AB). Une droite est illimitée.

Trois point sont alignés s'ils appartiennent à la même droite.

Les points E, F et M sont alignés. Le point M appartient à la droite (EF).

On écrit MÎ(EF).

Deux droites sont sécantes lorsqu'elles ont un seul point commun.

AÎd et AÎd'

2) Droites parallèles :

Deux droites distinctes sont parallèles si elles n'ont aucun point commun.

d//d': d est parallèle à d'.

3) Droites perpendiculaires :

Deux droites sécantes sont perpendiculaires si elles se coupent en formant un angle droit. D^D': D est perpendiculaire à D'.

4) Propriétés :

Si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles entre elles.

d^D et d'^D alors d//d'

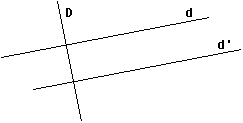
Si deux droites sont parallèles, alors toute droite perpendiculaire à l'une est perpendiculaire à l'autre.

d//d' et d^D alors d'^D

5) Constructions :

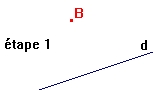
1) à la règle et à l'équerre d'une perpendiculaire à une droite donnée:

2) à la règle et à l'équerre d'une parallèle à une droite donnée:

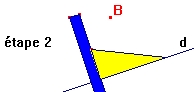
3) à la règle et au compas d'une parallèle à une droite donnée: