La propriété de Pythagore

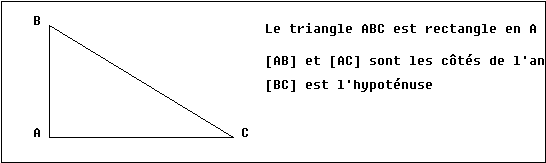
1) Le triangle rectangle:

Un triangle rectangle est un triangle ayant un angle droit.

Le côté opposé à l'angle droit est l'hypoténuse.

Dans un triangle rectangle le plus grand côté est l'hypoténuse.

2) La propriété de Pythagore:

Dans un triangle rectangle le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.

BC² = AB² + AC²

Remarques: Cette propriété ne s'applique qu'aux triangles rectangles!

Cette propriété permet de calculer la longueur d'un côté du triangle rectangle connaissant les deux autres.

L'usage de la touche de la calculette est souvent nécessaire.

Exemples:

ABC triangle rectangle en A avec AC=9 et BC=15. Calculer AB.

La propriété de Pythagore dans le triangle ABC rectangle en A donne: BC² = AB² + AC²; donc

15² = AB² + 9²

225 = AB² + 81 et AB² = 225 - 81 = 144

AB² = 144 donc AB =

3) Réciproque de la propriété de Pythagore:

Si dans un triangle, la carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés alors ce triangle est rectangle.

L'angle droit est l'angle opposé au plus grand côté.

Si dans un triangle ABC on a BC² = AB² + AC² alors ce triangle est rectangle en A.

Exemples:

a) Le triangle ABC avec AB=8 ; AC=18 et BC=20 est-il rectangle?

BC est le plus grand côté; on calcule BC² = 20² = 400

On calcule AB² + AC² = 8² + 18² = 64 + 324 = 388

Le triangle ABC n'est pas rectangle car BC² ¹ AB² + AC²

b) Le triangle MNP avec MN=3,3 ; NP=6,5 et PM=5,6 est-il rectangle?

NP est le plus grand côté; NP² = 6,5² = 42,25

MN² + MP² = 3,3² + 5,6² = 10,89 + 31,36 = 42,25

Le triangle MNP est rectangle en M car NP² = MN² + MP²