Les triangles

1) Tracé d'un triangle :

a) Connaissant les mesures des trois côtés :

Pour construire le triangle ROI de côtés RI=5 ; RO=4 et OI=6 , on trace le côté RI de 5cm puis l'arc de cercle de centre R et de rayon 4cm et enfin l'arc de cercle de centre I et de rayon 6cm .

b) Connaissant les mesures de deux côtés et de l'angle compris entre ces côtés :

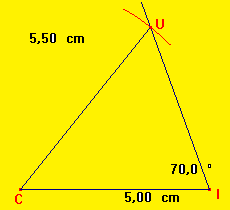
Pour construire le triangle CUI de côtés CI=5 ; CU=5,5 et

, on trace le côté CI=5cm puis , à l'aide du rapporteur , on trace l'angle de 70° de sommet I et enfin l'arc de centre C et de rayon 5,5cm .

c) Connaissant la mesure d'un côté et celles des deux angles adjacents :

Pour tracer le triangle LAC de côté LC=5 et d'angles

; on trace le côté LC=5cm et à l'aide du rapporteur on trace l'angle de 30° et de sommet C et enfin l'angle de 110° et de sommet L .

2) Inégalité triangulaire :

Dans tous les triangles, la mesure d'un côté est inférieure à la somme des mesures des deux autres côtés .

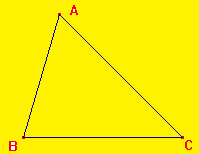
BC < BA + AC

AC < AB + BC

AB < AC + CB

Si BC=BA+AC alors le point A est un point du segment [BC] .

Si le point A est un point du segment [BC] alors BA+AC=BC .

Remarque: pour que trois mesures de côtés donnent un triangle, il faut que la somme des deux plus petits soit supérieure au plus grand.

Exemples : a) les trois longueurs de côtés suivantes donnent elles un triangle?

5, 7, 11.

les plus petits côtés sont 5 et 7, leur somme 5+7=12 est plus grande que le plus grand côté (11) donc ils forment un triangle.

b) les trois longueurs de côtés suivantes donnent elles un triangle?

8, 8 et 12.

les plus petits côtés sont 8 et 8, leur somme 8+8=16 est plus grande que le plus grand côté (12) donc ils forment un triangle.

c) les trois longueurs de côtés suivantes donnent elles un triangle?

6, 5 et 12.

les plus petits côtés sont 6 et 5, leur somme 6+5=11 est plus petite que le plus grand côté (12) donc ils ne forment pas un triangle.

3) Droites particulières d'un triangle :

Les médiatrices

(droites perpendiculaires aux milieux des côtés)

Les hauteurs

(droites passant par un sommet et perpendiculaire au côté opposé)

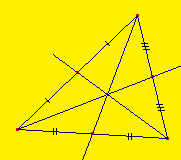
Les médianes

(droite passant par un sommet et le milieu du côté opposé)

4) Propriétés de la médiatrice :

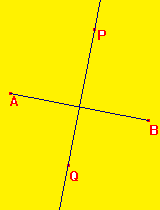
Si P appartient à la médiatrice de [AB] alors PA=PB .

Si PA=PB alors P appartient à la médiatrice de [AB] .

Si PA=PB et QA=QB alors (PQ) est la médiatrice de [AB] .

Si un point appartient à la médiatrice d'un segment alors il est équidistant des extrémités de ce segment .

Si un point est équidistant des extrémités d'un segment alors il appartient à la médiatrice de ce segment .

Si deux points sont équidistants des extrémités d'un segment alors la droite passant par ces deux points est la médiatrice de ce segment .

5) Première démonstration ; le cercle circonscrit au triangle :

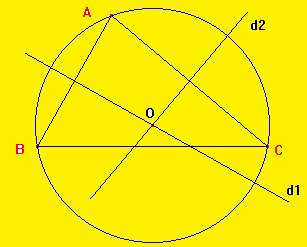
Dans tout triangle, les trois médiatrices se coupent en un même point .

Ce point est le centre d'un cercle passant par les trois sommets du triangle .

Ce cercle est le cercle circonscrit au triangle .

Démonstration :

(d1) est la médiatrice de [AB] donc O est équidistant de A et de B : OA=OB .

(d2) est la médiatrice de [AC] donc O est équidistant de A et de C : OA=OC .

Comme on a OA=OB et OA=OC on en déduit que OB=OC donc que O appartient à la médiatrice de [BC] . Les trois médiatrices se coupent en O .

On a OA=OB et OA=OC on en déduit que OA=OB=OC .

Le point O est équidistant de A, de B et de C, il est donc centre du cercle passant par A , B et C .